事实上，日光温室的围护结构内部的传热过程并非稳态，为了更为客观的掌握温室内部的热环境，就要进行墙体非稳态传热分析，进而了解墙体的热工性能及其热传导过程，进而改善其隔热保温措施，这对日光温室能耗分析来说是关键的一部分，有助于节能型日光温室设计和运用的发展。

一、墙体非稳态传热

墙体非稳态传热过程、墙体内部的温度分布以及热流量随着时间的变化规律的求解，实质上就是求解以下两个偏微分方程：上述两个偏微分方程的解法主要有以下两种：积分变换法和有限差分法。本文所关心的问题是墙体表面发生的温度和热流量变化，至于墙体内每个部位的具体温度变化则不必细究。日光温室围护结构的整个传热过程温度变化范围较小，可以将墙体导热系数又和导温系数Q当做是常数。因此，选择使用积分变换法来计算该常系数线性偏微分方程组定解问题。按照不同的边界条件分解方式，积分变换法可分为谐波反应法和瞬态反应法。由于太阳辐射等外部条件时刻发生变化，引起改变的不确定的因素时刻存在，难以用规律的正弦函数来描述，所以谐波反应法不可能作为持续性的能耗分析工具0瞬态反应法又包括Z传递函数法和反应系数法，两种方法都是把连续扰量离散成按时间序列进行分布的单元扰量。板壁的非稳态传热中，常见等腰三角波作为单元扰量，即要求获得板壁热力系统的Z传递系数或者反应系数，而两者具有相似的含义和求解方法。以下就分别对两种方法进行简单的介绍。

(1)反应系数法

反应系数法在求解问题时基本思路是，把随着时间连续变化的扰量曲线离散成为按时间序列进行分布的单元扰量；然后再求出墙体的热力系统对于单位单元扰量的反应系数；最后，运用已求得的反应系数叠加积分后算出单位面积板壁的围护结构逐时传热得热量。Mitalas和Stephenson提出并且详细介绍了反应系数法在负荷计算中起到的应用。墙体的反应系数序列YG)的定义是墙体对于其单位等腰温度的三角波输入热流所具有的输出值的等时间序列。它能够描述墙体受到室外温度扰量的动态响应过程，通过三角波的叠加来逼近室外空气综合温度变化情况，从而获得墙体热力系统对于任意室外扰量所产生的响应。反应系数法适用于任何一种扰量，它有别于谐波法的一个重要的特点就是，反应系数法并不要求边界条件具有周期性，因此它可以用于全年性的动态模拟。为了获得反应系数，需要对墙体传热或者吸热传递函数的分母B(s)求根，也就是求出s传递函数的极值点，然后运用Heaviside展开式求解得到最终的结果，通常称为直接求根法。但B(s)有无穷多个负实根(-s.)，所以求出所有的根是不现实的。根小到一定程度时，其对反应系数产生的影响非常微小，一般只需求得一定数量的根值，就可以保证反应系数所具有的精度负荷要求。通过计算和比较，我们发现，计算Y(0}和Y(1)时，取传递函数法的理论基础是由当前的输入值和前一时刻的输入值和输出值共同确定。

和反应系数相同，传递函数也能够描述墙体动态热特性，但是所需求的系数项比起反应系数来说少得多，这就使得计算所耗费的时间和计算机存贮空间大大的减小。系统的z传递函数，也即脉冲传递函数，其实是系统单位脉冲响应的z变换。但这里所说到的板壁围护结构z传递函数，是指板壁热力系统的单位等腰三角脉冲产生的响应的z变换，相当于系统中设置了单位等腰三角波保持器。所以，板壁围护结构传热和吸热的z传递函数，指的就是板壁吸热和传热反应系数序列的z变换。相比于其他的方法，传递函数法最为重要的性质就是其输入输出的值是等时间间隔序列值。因此，作为输入值，太阳辐射强度和室外温度的逐时记录数据，只需要做很少的预处理。此方法主要的局限性是它只能够用于线性时不变的系统；而传递函数则可以通过直接求根法来求解墙体的吸热或传热z传递函数来获得，尽管直接求根法不可避免的失根现象在这里仍然存在；z传递函数作为反应系数的近似形式，必然会导致一定的误差。综合上述三种常用墙体非稳态传热的计算方法各自的优缺点，本文决定运用反应系数法来进行墙体非稳态传热的计算。

二、反应系数计算法

(1)扰量的离散

用等腰三角波来进行扰量的离散，能够将室外气候的变化规律较为精准的表达。

三、定义非稳态边界条件选取8月30日早9：00^-16：30作为非稳态计算的时间段。计算域的确定、网格的划分、控制方程及模拟模型的相关设置都与稳态模拟相同，主要边界条件的设置为：以上边界中除了需要用自定义函数(UDF)来定义的非稳态边界条件而外，其余边界条件的确定均与稳态数值模拟时相同，这里不再重复了。下面着重的介绍非稳态边界条件中入口温度、膜以及土壤边界条件的设置情况。因为早9：00—16：30这个时段入口温度、膜、土壤温度和后墙风口里来自室外的新风温度波动度都比较大，膜温随着太阳辐射强度的变化也一直在改变，所以定义为定温或者绝热边界都与实际的情况具有较大的差距。并且这些温度都具有一定的变化规律，早晚较低而中午较高，即与时间t存在密切的关系。上述五个回归程式的相关系数分别为0.9833，0.9633，0.9843，0.9799，0.9044，说明所测入口温度、膜、土壤温度、后墙温度、后墙风口温度与时间呈显著相关，因此可以用上述五式表达入口温度、膜、土壤温度、后墙温度、后墙风口温度随时间的变化规律。将土述五个回归方程式使用c语言源代码表达出来，建立一个c语言源代码文件，编译UDF函数并连接到FLUENT，在FLUENT中执行UDF，进行计算，详见附录。

三、三维稳态计算结果与分析

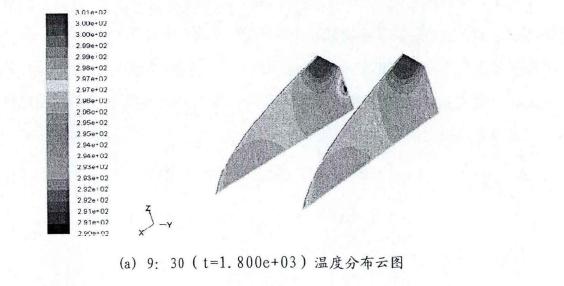
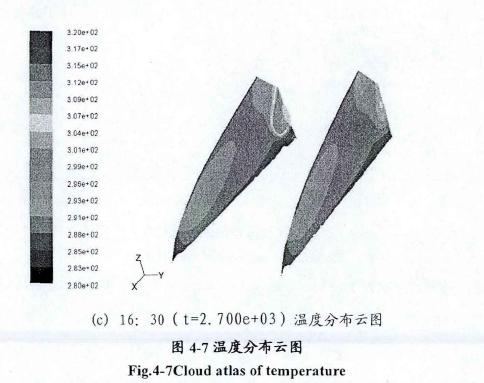
设置完非稳态边界条件以后，仍然取1e-3作为计算动量方程、连续性方程、k及￡方程时的收敛精度标准，辐射和能量方程的计算收敛精度标准为1e-6。迭代计算的步长值设为60s，每个步长内最大迭代次数取80次，每问隔30min自动保存当前时刻的计算结果。图4-7给出了9：30，13：30与16：30温度场的计算结果，分别选Y=1800mm(对准风口)、Y=6300mm(两风口之间)两个截的温度值来进行比较分析。图4-7反映出了温室两个具有代表性的剖面在不同时刻呈现出的温度分布云图。

本次非稳态模拟从初始时刻9：30开始到16：30结束，以上分别选择了上午9：30(t=1.800e+03)、中午13：30(t=1.6200e+03)、下午16：30(t=2.7000e+03)三个时刻的温度分布云图来进行分析。由图中能看出：从9：30到13：30温室内温度逐步升高，薄膜附近的室气温度变化幅度较大；到16：30时，室内空气较13：30已经有了明显的降低，这与实测结果吻合，在第二章中我们看到，16：00过后室外温度开始呈下降趋势。模拟的结果进一步验证了太阳辐射是导致温室内空气温度上升的主要原因。比较不同时刻的温度分布云图能够看出，不同时刻室内空气温度沿高度Z方向的布有所不同，但基本规律相似，最高温都出现在温室顶部，这是由于空气受到热浮力往高处上升，并且通过前后风口进入室内的新风在室内吸取热量后经风压作用由顶部窗口排出。与测试数据相比较可知，整个计算空间的模拟得到的温度分布趋势和实测数据的规律基本相同。

四、实验数据验证非稳态模拟结果

在上午9：30的模拟结果中取出试验测点处的温度值与实测值做比较，如图4-8所示，从图4-8中可以看出，三维非稳态的模拟结果能够准确的反应出温室内不同点的温度变化趋势。模拟的结果整体比试验数据偏小，最大误差为3.04℃，位于下端靠近土壤表面处，最小误差仅为0.001℃。造成模拟值偏小于实测值的原因，主要是室外气候的随机以及多变性在时刻改变自然通风口的空气流动方向、速度大小、风量和温度等，使得在本次模拟计算中，边界条件很难精确的符合实际情况。

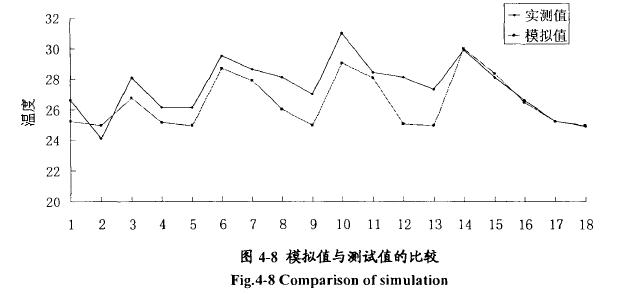
从图中我们可以看到，虽然模拟结果显示的温室内空气温度分布与实测值在数值上存在一定差异，但除了边界点外，最大误差仅在2.2℃以内；并且空间分布的总体趋势是一致的，所以本次对日光温室热环境的三维非稳态数值模拟是成功的。相比于稳态数值计算结果，非稳态数值模拟结果与实测值的吻合程度更高。所以，得出结论：本章节建立的三维非稳态CFD模型及包括的边界条件有效，利用fluent来进行夏季自然通风条件下日光温室的热环境三维非稳态数值计算是可行的。http://www.zhenghangsy.net